Desviación media
En estadística la desviación absoluta promedio o, sencillamente desviación media o promedio de un conjunto de datos es la media de las desviaciones absolutas y es un resumen de la dispersión estadística. Se expresa, de acuerdo a esta fórmula:
La desviación absoluta respecto a la media, 
, la desviación absoluta respecto a la mediana, 
, y la desviación típica, 
, de un mismo conjunto de valores cumplen la desigualdad:
, la desviación absoluta respecto a la mediana, , y la desviación típica, , de un mismo conjunto de valores cumplen la desigualdad:
Siempre ocurre
donde el Rango es igual a:
El valor:
ocurre cuando los datos son exactamente iguales e iguales a la media aritmética. Por otro lado:
cuando solo hay dos valores en el conjunto de datos.
Desviación respecto a la media
Como su nombre indica, la desviación respecto a la media da información de lo alejado o cerca que está un dato de los demás datos del conjunto. Intuitivamente, ya se ve que se puede calcular como la diferencia entre un dato y la media de los datos:
Se puede observar que para calcular esta desviación, si se dispone de la media, sólo se requiere aquel valor la desviación del cual se quiere calcular.
También cabe comentar que teniendo uno de los datos y su desviación respecto a la media, se puede despejar la media aplicando una simple resta:
y posteriormente usarla para calcular las demás desviaciones.
Ejemplo
En el examen de matemáticas Pedro ha sacado un 9 , la media de la clase es de 6.7 . Calcular la desviación respecto a la media de la nota de Pedro.
Aplicando la fórmula
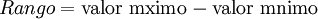
No hay comentarios:
Publicar un comentario